Mi chiamo Roberto Tognelli, sono di Pistoia e ho due passioni principali: l’informatica, che è anche la mia occupazione professionale di tutti i giorni, e l’astronomia amatoriale, che pratico da 40 anni esatti “sul campo” con l’amico d’infanzia Nicola, membro del Gruppo WoO e più stretto collaboratore, e da un po’ meno sul piano teorico con l’aiuto del computer. Ma forse la mia vera passione – come informatico – è mettere in ordine il mondo; non a caso i francesi chiamano il computer ordinateur, cogliendo il senso dell’informatica molto meglio di noi che invece lo chiamiamo calcolatore, quando se i computer hanno un problema, quello consiste proprio nel gestire i numeri a livello nativo.

A Torri ho avuto il piacere, quest’estate, di condurre un paio di incontri divulgativi nei quali abbiamo illustrato l’aspetto del cielo estivo agli intervenuti, facendo anche un po’ di discorsi di astronomia teorica. La divulgazione scientifica è l’altro grande tema di interesse, per me, in un momento storico nel quale nonostante la pervasività della tecnologia e quindi della scienza che necessariamente la alimenta, la gente sembra spesso continuare a ignorare se non respingere anche concetti elementari della scienza stessa, per non parlare della incapacità di troppe persone di farsi un’idea dei concetti di grandezza, di misura, di probabilità che un evento accada o non accada, di errore e via dicendo. Pensate a voi stessi e a tutti gli errori che vi sarà capitato di fare quando avete provato a stimare una distanza… 🙂

Quello che voglio proporre qui, in effetti, è una sorta di assaggio di tema scientifico, da prendersi come un invito a proseguire questi incontri di divulgazione unitamente a eventi locali, caratteristici del territorio, nella speranza di contribuire a far diventare Torri un centro di attrazione che unisca i piaceri offerti dal territorio stesso con alcuni temi della divulgazione scientifica, del pensiero razionale, del piacere della scoperta.

In occasione del ritrovo del 10 dicembre per l’osservazione delle Geminidi ho pensato di proporre qualcosa che legasse Torri al cielo, in qualche modo.
Ed ho trovato questa idea, che tutto sommato ritengo elegante perché, benché totalmente priva di ogni aspetto pratico, riunisce in se molte basi del ragionamento scientifico e di diverse tecniche che, volendole sviscerare compiutamente, formerebbero da sole il materiale per diverse conferenze su temi di astronomia, di informatica, di calcolo. E parla strettamente di Torri, come vedrete.

E parla dei fondamenti della nostra cultura scientifica e tecnologica, se volete.

Mi sono chiesto: come posso legare un pezzetto di terra a qualcosa del/nel cielo?

Esiste una corrispondenza possibile, un legame tra un luogo sulla terra e qualcosa che riguarda la meccanica celeste, sia essa rappresentata da un corpo, da una legge, o da una storia?

E mi è subito parso naturale, intanto, cominciare a legare un pezzo di terra, Torri, con quello che in cielo è esattamente sopra di esso, geometricamente. Questa cosa in astronomia si chiama zenith: lo zenith è quel punto del cielo esattamente sulla verticale del luogo scelto. In pratica tirate una riga dritta dal centro della Terra a Torri e proseguite verso l’alto: dove la vostra retta buca la volta celeste, quello è lo zenith.

Dunque, come per ogni altro luogo della terra, anche Torri ha uno zenith. Sì, ma, un attimo: parlavamo di una retta, qualcosa di… sottilissimo. Qualcosa che più che con un luogo potrebbe essere messo in relazione con un punto, un punto esatto del paese. E qual è il punto che caratterizza il paese?

Classicamente, almeno qui in Europa, fin da tempi remoti ogni centro abitato è sicuramente rappresentato al meglio dal suo campanile. Il campanile rappresentava un buon punto di riferimento, in passato, anche perché ben visibile da abbastanza lontano: si usavano infatti i campanili per triangolare il territorio e attribuire coordinate geografiche ai vari luoghi. Ad esempio, prima di Google Maps e dei GPS il campanile della cattedrale di Pistoia rappresentava il punto geografico di coordinate 43° 55’ 58” – 10° 56’, mentre oggi Google Maps fornisce 43° 56′ 0.143″ N, 10° 55′ 03″ E, segno che qualche evoluzione c’è stata…

Dunque, focalizziamo sullo zenit del campanile di Torri.
Vi risparmio i numeri, ma vi dico che ho reperito le coordinate del campanile sulla rete con un errore che posso stimare dell’ordine del metro. E un metro a quanto equivale, in cielo? Ha senso dire “un metro”, parlando di una distanza che applico alla volta celeste?

Ovviamente no: in cielo si misura tutto in gradi. Proviamo a impadronirci del meccanismo.

Immaginate di essere nel mare e avere tutto l’orizzonte libero. Immaginate un arco che passa esattamente sopra la vostra testa (il vostro zenith) e poggia sul punto est e sull’ovest. Questo arco misura 180°, perché rappresenta “mezzo cielo”, mezzo angolo giro, la metà del cielo intero, cioè di 360°. Questa sarà la nostra base di partenza. Ogni distanza tra corpi celesti la si misurerà usando frazioni di questo arco o, se volete, aprendo un compasso o goniometro immaginario il cui centro sarà il vostro occhio (o meglio il centro della terra) e le cui punte saranno rivolte verso i corpi di cui vogliamo esprimere la distanza.

Ma veniamo a qualcosa di pratico, qualcosa che conosciamo tutti, per avere un riferimento più intuitivo: la Luna. La Luna PIENA misura quasi esattamente mezzo grado di diametro, ed è un buon riferimento per confrontare distanze in cielo. Se immaginate l’arco di cui prima costellato di lune piene, ce ne starebbero 360, da orizzonte a orizzonte, vi torna?

Ora, l’arco di 180° in questione copre un intero meridiano terrestre, che è di circa 20.000 km. Se fate la divisione avrete che un grado corrisponde alla proiezione in cielo di circa 111 km. La Luna piena, mezzo grado, circa 56 km. Quindi, se proiettate in cielo un cerchio di terra di 56 km di diametro, esso coprirebbe quasi esattamente la luna. Dunque, il metro di cui parlavamo prima coprirebbe 1/56.000 del diametro della Luna…

Allora: se proietto in cielo il campanile di Torri ottengo un quadratino di lato, diciamo, circa 20.000 volte più piccolo della Luna, con l’errore potenziale suddetto.

Mi domando: ci saranno stelle, lì dentro? O, magari, stelle importanti?

Ci sono in cielo circa 6.000 stelle visibili a occhio nudo, ma molte, molte di più a noi invisibili, solo nella nostra galassia.

Ma qualche stella importante cadrà sul nostro campanile? O nei dintorni, magari…?

Per inciso: cosa vuol dire stella importante?

Una stella è sicuramente importante se è molto luminosa, e quindi conosciuta dall’antichità, legata a miti e storie varie, elemento determinante di una costellazione; ma può anche essere al limite della visibilità o del tutto invisibile e avere caratteristiche fisiche o chimiche di rilievo. Ad esempio, la stella di Barnard, in Ofiuco, è decisamente invisibile a occhio nudo, ma sappiamo che è la stella più veloce tra quelle conosciute: nell’arco di una vita umana copre una distanza pari alla metà del diametro della luna piena.

Torniamo a noi: passano stelle importanti sul nostro campanile, in capo al giorno astronomico?

Il cielo gira (come effetto della rotazione della Terra).

In capo al giorno e all’anno, dunque, una “striscia di cielo” passa sul nostro campanile.

Quello che dovrei cercare è: quali stelle hanno una altezza sull’equatore tale da rimanere in quella striscia, in modo che in capo al giorno e all’anno, passino sopra di noi.

Per fare le cose fatte bene, va detto che i cataloghi stellari moderni contemplano 1.800.000.000 stelle circa. Fare una ricerca manuale sarebbe proibitivo… Né ha senso pensare che una delle 6.000 stelle visibili a occhio nudo ricada nel quadratino di cielo suddetto, per ovvie ragioni di probabilità (fatti i conti abbiamo una probabilità di trovarvi una stella in capo alla giornata di circa 1:1.080)

Allora mi serve del software: un programma che consideri tutte le stelle e una a una verifichi se mai quella passa dal quadratino…

Scarico tutto il catalogo (1,3 Tb compresso!) e scrivo personalmente un programma; che, a questo punto, non scrivo espressamente per il caso Torri, bensì per una località qualsiasi del pianeta, e per un intorno di lato arbitrario…

Tenete conto che il database di stelle che ho scaricato, il più completo (Gaia versione 3.0), contiene un sacco di roba, compresi i parametri fisici delle stelle, la composizione, i moti propri…

Solo la riduzione dei dati al set sufficiente per la mia ricerca ha impiegato circa 33 ore…

E poi, finalmente, i risultati.

Considerando il campanile come un quadrato di lato 4 metri, sulla sua proiezione in cielo statisticamente passerebbero circa 400 stelle in capo alle 24 ore del giorno medio. Ne trovo invece 228, nel nostro caso specifico; ma di queste, nessuna la cui magnitudine superi quella di Plutone (quasi tutte magnitudine 20, roba al limite della visibilità coi più grossi telescopi).

Allora allargo un pochino il campo: considero un corridoio di 1 km, che sicuramente ingloba tutte le case del paese. Ci trovo circa 50.000 stelle. Le ordino per distanza dal campanile e per magnitudine.

Tra queste, a soli 6,40 metri a sud del centro del campanile (praticamente sulla cuspoide del tetto della canonica!) c’è una stella di magnitudine 8,70 (quindi invisibile a occhio nudo) dal nome decisamente irrilevante: “Gaia 373512591107946112”.

La stella più luminosa nei pressi del paese è invece una stellina di magnitudine 6.40 (anch’essa invisibile) che passa 482 metri a sud del campanile, e dunque “in pieno bosco”. Altro non c’è, di interessante.

Dunque, Torri non ha una stella clamorosa, al suo zenith; ma, come dicevamo, l’importanza di una stella non è che soggettiva, alla fine, e sicuramente è determinata solo dalla nostra posizione nello spazio. Provo allora a immaginarmi quella stella da vicino: magari possiede pianeti sui quali è fiorita la vita, e chissà cos’altro; e immagino che creare un gemellaggio con un corpo celeste sul quale oltre a poche misure di luce e di distanza si possa lavorare solo con la fantasia, può avere un senso… 🙂

Ed eccola, la stellina di Torri: è nella costellazione di Andromeda, a poca distanza dall’omonima galassia.

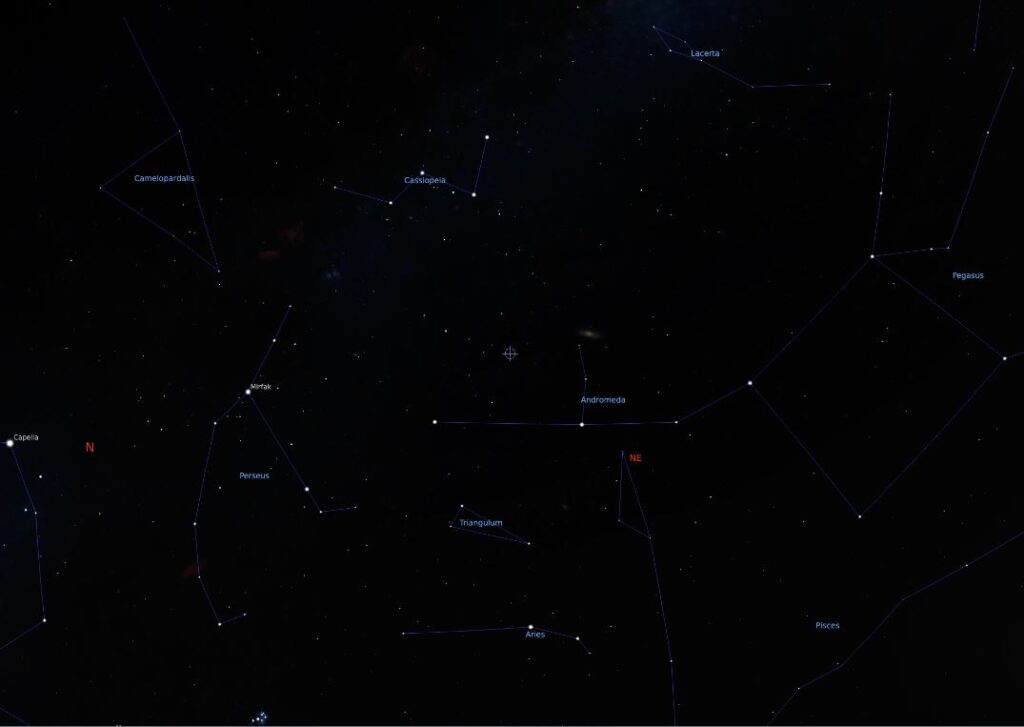
Culmina sullo zenith di Torri verso la mezzanotte del 30 ottobre.

Se volete cercarla su Stellarium, le sue coordinate celesti sono: A. R. 19.369014, Dec. 44.06479535.

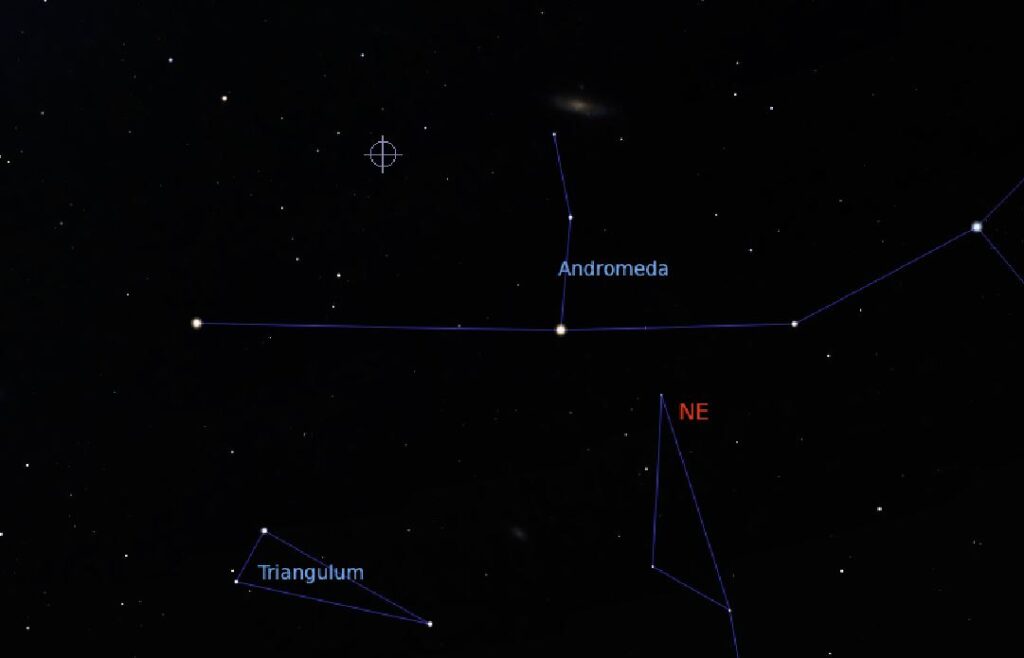
Grazie a tutti!